39 phase diagram degrees of freedom

The Gibbs phase rule tells me that at a substance's triple point, where there are 3 phases in equilibrium, there should be 0 degrees of freedom. Based on my understanding, that means there should be 0 intensive properties that can be varied. When you look at a P-T phase diagram, the triple point is actually a point so the 0 DF makes sense.

Phases, components, degrees of freedom For the description of multicomponent equilibrium system there is a general connection between the degrees of freedom (F), the number of the components (C) and the number of the phases (P) called Gibb's phase rule: P + F = C + 2. (6.1.) Expressing the degrees of freedom F = 2 + C - P .

Our ternary diagram has three vertices (S,X,W), and defining any 2 of these defines the last. Hence the phases in the diagram only have 2 Degrees of Freedom. In practice, the Degrees of Freedoms is = (number of axes plotted – 1). So for our ternary phase diagram, F=2, C=3. Our maximum number of Phases is P=3. What does this mean?

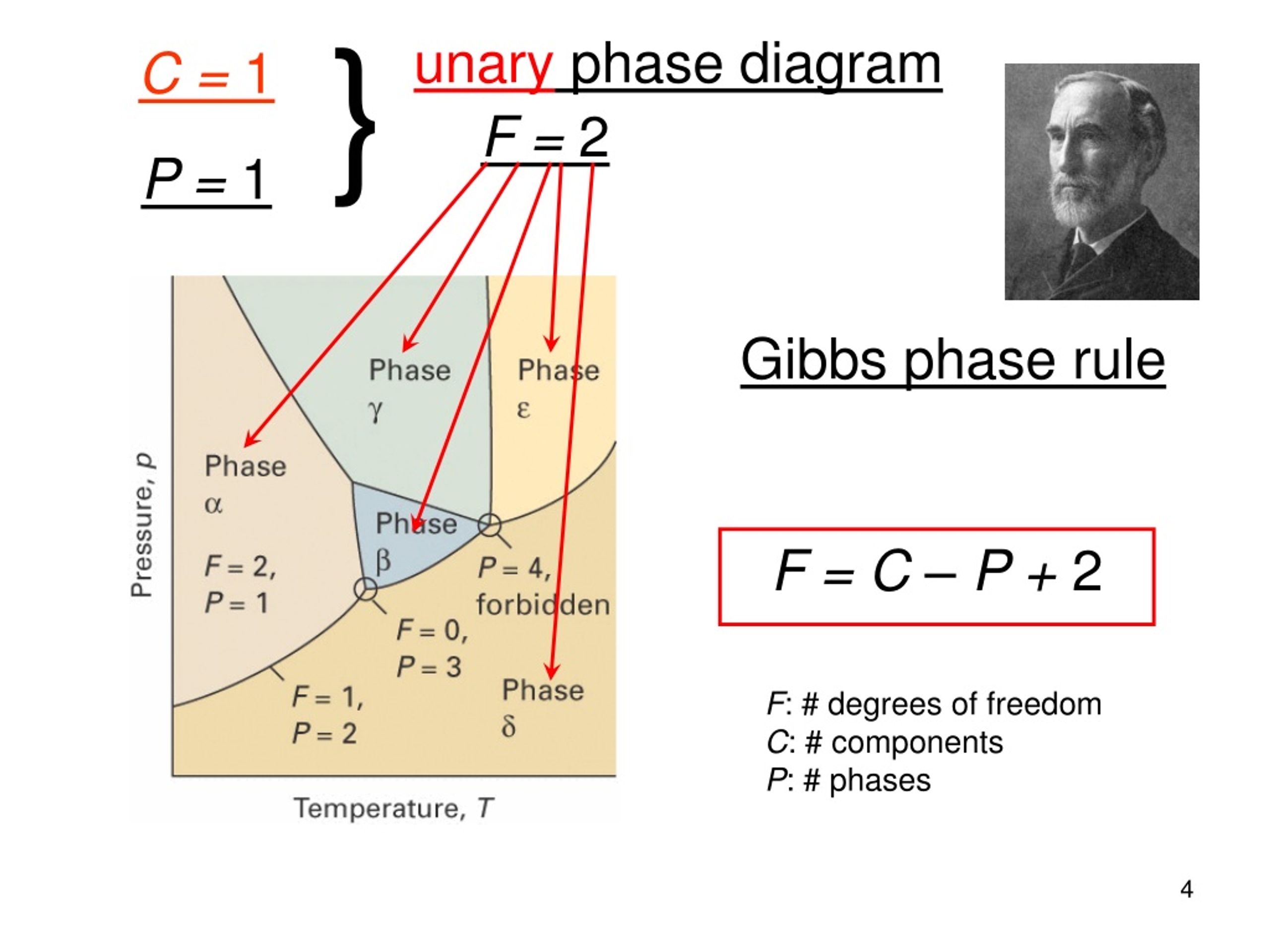
Phase diagram degrees of freedom

Phase rule states that " If the equilibrium between any number of phases is not influenced by gravity, or electrical, or magnetic forces, or by surface action but are influenced only by temperature, pressure and concentration , then the number of degrees of freedom (F) of the system is related to the number of

One of these two remaining degrees of freedom is the pressure and the other is the composition (expressed by the mole fraction of one component. One form of the phase diagram - a map of pressures and compositions at which each phase is stable and the other - a map of temperatures and compositions. Relevant to geology

PHASE EQUILIBRIA n Number of Components and Degrees of Freedom 6.1. The region marked orthorhombic is a single-phase region. Since this is the phase diagram for pure sulfur, there is only one component. From the phase rule f = c - p + 2, with c = 1 and p = 1, the value of f is: f = 1 - 1 + 2 = 2. The two degrees of freedom are pressure and ...

Phase diagram degrees of freedom.

People also ask, what is degree of freedom in phase diagram? The 'degrees of freedom' of the system (at chemical equilibrium) refer to the number of conditions or variables that can be altered, independent of each other, without effecting the number of phases in the system. One may also ask, what is phase rule equation?

Chapter 8 2 Phase diagram and “degrees of freedom” A phase diagrams is a type of graph used to show the equilibrium conditions between the thermodynamically-distinct phases; or to show what phases are present in the material system at various T, p, and compositions

The phase rule, also known as the Gibbs phase rule, relates the number of components and the number of degrees of freedom in a system at equilibrium by the formula F = C - P + 2 [1] where F equals the number of degrees of freedom or the number of independent variables, C equals the number of components in a system in equilibrium and P equals

At B there are three possible phases (gas, liquid, and solid) and consequently the degrees of freedom of the system is 0 (ie B is a critical point). Similarly we can find at C the degrees of freedom to be one because there are two possible phases (fluid or solid) as indicated by the red line drawn through C.

Phase Diagrams Best, Chapter 14 Gibbs Phase Rule F = 2 + C - ϕ F = degrees of freedom (P-T-X) C= components ϕ = phases Degrees of Freedom • Rule applies to a phase or assemblage • Divariant indicates two degrees of freedom • Univariant means one degree of freedom • Invariant means there are no degrees of freedom Petrogenetic Grid • The grid define stability limits – End-member ...

For a binary phase diagram plotted at 1 bar, where composition is displayed on the abscissa and temperature on the ordinate, the number of components c equals two, and the Gibbs phase rule is then f=3−ϕ.In a single-phase region, the number of degree of freedom equals 2, meaning that the two state variables temperature and composition may be varied independently.

For an azeotropic binary mixture, the number of phases is 2 and number of components are 2. So, according to Gibbs phase rule, the number of degrees of freedom should be 2. But, the right answer is 1. Can someone explain this? physical-chemistry thermodynamics phase Share Improve this question asked Feb 16 '18 at 4:05 Sriram Krishnamurthy 146 1 6

Gibbs Phase Rule degree of Freedom (example)Subscribe to my channel:https://www.youtube.com/c/ScreenedInstructor?sub_confirmation=1Workbooks that I wrote:htt...

In thermodynamics, the phase rule is a general principle governing "pVT" systems (that is, systems whose states are completely described by the variables pressure (p), volume (V) and temperature (T)) in thermodynamic equilibrium.If F is the number of degrees of freedom, C is the number of components and P is the number of phases, then = + It was derived by American …

According to the phase rule, a one component system has no degrees of freedom when three phases are in equilibrium (F=0).The system is invariant. The triple point of water is at 273.16 K and 612 Pa. Phase diagram for water showing the triple point of water. This is an invariant point. This phase diagram is from Wikipedia. Binary systems

degrees of freedom (F) by Gibbs phase rule. Degrees of freedom refers to the number of independent variables (e.g.: pressure, temperature) that can be varied individually to effect changes in a system. Thermodynamically derived Gibbs phase rule: In practical conditions for metallurgical and materials

Once the phase integral is known, it may be related to the classical partition function by multiplication of a normalization constant representing the number of quantum energy states per unit phase space. This normalization constant is simply the inverse of Planck's constant raised to a power equal to the number of degrees of freedom for the ...

Ppt - phase diagrams of m ixtures of compounds powerpoint ...

Answer: a. Clarification: The number of degrees of freedom is the number of variables in a set of independent equations to which values must be assigned so that the equations can be solved. 2-3. For degrees of freedom (Nd) expression, Nd = Nv - Ne. 2. Nv represents. a) Number of variables. b) Number of equations.

Pdf télécharger phase diagram pdf gratuit pdf | pdfprof.com

According to Gibbs Phase Rule, at this phase transition, we know that the number of degrees of freedom is <math>F=\left( C+2-P \right)=2+2-3=1 </math>. There is only one degree of freedom, so if we assume constant pressure (a typical choice), then all three phases can only be in equilibrium at an invariant point--- the eutectic point! This ...

Solved indicate on the phase diagram of the-binary mixture ...

The composition of both the phase can, therefore, be expressed in terms of the same chemical individual NH 4Cl. Phase Components Solid = NH4Cl Gaseous = x NH3 + x HCl or x NH4Cl Thus dissociation of ammonium chloride is a one-component system. DEGREES OF FREEDOM The term Degree of Freedom represented by F in the phase Rule equation (F = C - P ...

Ppt - 5.5 phase diagrams of three-component systems ...

The number of degrees of freedom (number of variables we can change without affecting the “nature” of the system) is determined by the equation known as the phase rule: f = c – p + 2, (6.2) where f is the no. of degrees of freedom, p is the number of phases present and the “2” represents the two variables temperature and pressure. Applying this rule to a one-component phase diagram ...

Use gibbs phase rule to determine the degrees of freedom in a ...

Gibbs Phase Rule: f = c - p + 2 f = Intensive Degrees of freedom = variance Number of intensive variables that can be changed independently without disturbing the number of phases in equilibrium p = number of phases gas, homogeneous liquid phases, homogeneous solid phases c = components Minimum number of independent constituents Case I.

Equilibria involving condensed matter - ppt download

Prepared for submission to JHEP The chiral Gross-Neveu model on the lattice via a Landau-forbidden phase transition Gertian Roose,a Jutho Haegeman,a Karel Van Acoleyen,a Laurens Vanderstraeten,a and Nick Bultincka;b aDepartment of Physics and Astronomy, University of Ghent, Krijgslaan 281, 9000 Gent, Belgium bRudolf Peierls Centre for Theoretical Physics, …

Degrees of freedom

Hence the system has three degrees of freedom. From the definition, a gas or vapour may be completely defined by fixing two variables P and T or V because the third variable may be calculated from the equation PV = RT and will have a certain definite value ( R is a constant), hence the degree of freedom of the system is two.

Draw the phase diagram of one component system and find out ...

having two degrees of freedom, and the phase rule says that only one phase can exit in stable equi- librium (p = 1 - 2 + 2). This situation is called bivariant equilibrium. Binary Diagrams If system being considered comprises two components, a composition axis must be added to the PT plot, requiring construction of a three-

Phase diagrams a phase is a state of

1. outline phase rule what is meant by phase what is meant by components degrees of freedom derivation one component system phase diagram 2. phase rule the phase rule is an important generalization dealing with the behavior of heterogeneous system.

Chapter 8. phase diagrams - pdf free download

The phase rule states that F = C − P + 2. Thus, for a one-component system with one phase, the number of degrees of freedom is two, and any temperature and pressure, within limits, can be attained. With one component and two phases—liquid and vapour, for example—only one degree of freedom exists, and there is one pressure for each temperature.

Qmd model phase diagram without baryonic degrees of ...

14.11.2016 · There is only one unique place on this diagram where all three phases can coexist in equilibrium--the invariant point at 3.8 Kb and 500 o C; at this point there are zero degrees of freedom. There are three univariant reactions on this diagram, each representing the phase transitions: andalusite = sillimanite, andalusite = kyanite, and kyanite = sillimanite.

Solved given the adjacent txy phase diagram, apply the gibbs ...

In other words, two degrees of freedom represent two-dimensional regions (areas) on the Phase Diagram in which a single phase exists. Now, let’s consider the occurrence of two phases coexisting simultaneously (P = 2) in equilibrium. From Equation 2.04 with P = 2, we have one degree of freedom (F = 1).

The phase rule

Determine the degrees of freedom under the following conditions: (a) Tl-20 wt% Pb at 325 °C and 400 °C; (b) Tl-40 wt% Pb at 325 °C and 400 °C ; (c) Tl-90 wt% Pb at 325 °C and 400 °C. Refer to the phase diagram in Figure 10-8(d).

Engarc - l - gibbs phase rule

The Gibbs phase rule is f = c − p + 2, where f is the degrees of freedom, c is the number of components, and p is the number of phases. Your diagram says P = c s t, which I interpret to mean that pressure is constant. That specification lowers the number of degrees of freedom by one, so f = c − p + 1.

Degrees of freedom

Degrees of Freedom. ... This shows qualitatively a very simple phase diagram for a given material. The liquid, solid, and gas phases are separated by curves in the T,P parameter space. On these curves, both phases are represented to some degree simultaneously.

Why does an area in phase diagram considered as having degree ...

The extend of each phase corresponds to one degree of freedom. Thus, we have to subtract Pfrom f total. (7.38) This result is known as the Gibbs phase rule. With one phase, C = 1, R = 0, P = 1, we have two degrees of freedom, pressure and temperature.